Identifizierung von Scheinkorrelationen
Johannes Lüken / Dr. Heiko Schimmelpfennig
Kontrolle von Störvariablen mit der Regressionsanalyse
Ein statistischer Zusammenhang wie beispielsweise eine positive Korrelation zwischen Produktqualität und Kundenzufriedenheit genügt allein nicht, um die Produktqualität als Treiber der Zufriedenheit zu identifizieren. Es muss zudem ausgeschlossen sein, dass dieser statistische Zusammenhang auf Störvariable(n) zurückzuführen ist. So könnte etwa das Markenimage beide Größen beeinflussen und damit die Korrelation zumindest zu einem Teil hervorrufen. Anhand eines kleinen leicht nachrechenbaren Zahlenbeispiels wird veranschaulicht, wie mithilfe der Regressionsanalyse der Einfluss einer Störvariable auf Ursache und Wirkung eines vermuteten kausalen Zusammenhangs kontrolliert und somit eine Scheinkorrelation aufgedeckt werden kann.
Lineare Regressionsanalyse
Mit der Regressionsanalyse wird die Abhängigkeit einer metrischen Variable (Regressand) von einer oder mehreren metrischen und/oder dichotomen Variablen (Regressoren) untersucht. Für jeden Regressor bestimmt sie einen Koeffizienten, der dessen Einflussstärke auf den Regressanden misst. Damit lässt sich eine Regressionsfunktion aufstellen, mittels der für jeden Fall der Stichprobe auf Basis der beobachteten Werte der Regressoren ein Wert des Regressanden berechnet (prognostiziert) werden kann. Die Differenz zwischen dem prognostizierten und dem beobachteten Wert des Regressanden ist das Residuum. Die Regressionskoeffizienten werden so berechnet, dass die Summe der quadrierten Residuen über alle Befragten minimiert wird (Ordinary Least Square (OLS)-Schätzung).
Zahlenbeispiel zur Kontrolle einer Störvariable
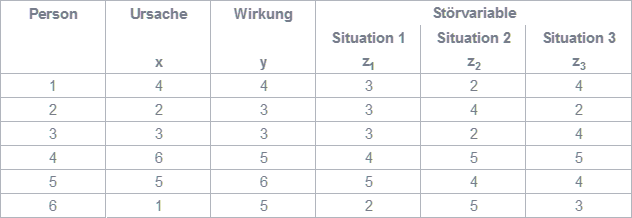
Vermutet wird, dass ein kausaler Zusammenhang zwischen der Ursache x und der Wirkung y besteht. Bei sechs Befragten wurden Werte dieser beiden Variablen erhoben (siehe Abbildung 1). Die Korrelation zwischen x und y beträgt 0,44. Für die Korrelationen einer möglichen Störvariable mit der Ursache und Wirkung werden im Weiteren drei Situationen unterschieden.
Abbildung 1: Zahlenbeispiel
Situation 1: z1 korreliert mit Ursache und Wirkung. Mit Hilfe jeweils einer einfachen Regression wird der Teil der Ursache beziehungsweise der Wirkung berechnet, der allein durch die Störvariable determiniert ist. Als Regressionsfunktionen ergeben sich für das Beispiel:
x = -1,5 + 1,5z1 und y = 2,25 + 0,625z1
Die Residuen für x und y spiegeln dann die Werte der Ursache beziehungsweise der Wirkung wider, die nach Herausrechnen des Einflusses von z1 übrig bleiben. Die Korrelation dieser Residuen ist allerdings 0. Demnach ist der positive statistische Zusammenhang zwischen Ursache und Wirkung vollständig auf den Einfluss der Störvariable auf die beiden Variablen zurückzuführen. Die Korrelation von 0,44 zwischen x und y ist eine Scheinkorrelation.
Der Umweg über die Berechnung der Residuen ist jedoch nicht notwendig, um den Einfluss der Störvariable auszuschalten. In einer multiplen Regression gibt ein Regressionskoeffizient die Veränderung des Regressanden an, wenn sich der Wert des Regressors um eine Einheit verändert – bei Konstanz der übrigen Regressoren. Um Regressoren mit unterschiedlichen Skalierungen vergleichbar zu machen, wird der standardisierte Regressionskoeffizient berechnet. Eine multiple Regression mit der Ursache und der Störvariable als Regressoren sowie der Wirkung als Regressand führt zu einem standardisierten Regressionskoeffizienten der Ursache von 0 (siehe Abbildung 2). Das heißt bei konstanter Störvariable verändert sich y nicht, wenn sich x ändert. Damit besteht zwischen Ursache und Wirkung offensichtlich kein kausaler Zusammenhang.
Abbildung 2: Korrelationen (Standardisierte Regressionskoeffizienten) in Situation 1
Situation 2: z2 korreliert nur mit der Wirkung. Der standardisierte Regressionskoeffizient der Ursache in der multiplen Regression ist gleich 0,44 (siehe Abbildung 3). Das heißt er ist genauso hoch wie die Korrelation zwischen Ursache und Wirkung. Trotz ihres Einflusses auf y ist z2 somit keine Störvariable, die den statistischen Zusammenhang zwischen Ursache und Wirkung beeinträchtigt.
Abbildung 3: Korrelationen (Standardisierte Regressionskoeffizienten) in Situation 2
Situation 3: Im Vergleich zu Situation 1 ist die Korrelation zwischen Störvariable (z3) und Ursache gleich, die Korrelation zwischen Störvariable und Wirkung aber geringer. Der standardisierte Regressionskoeffizient der Ursache ist in der multiplen Regression mit 0,28 positiv (siehe Abbildung 4). Insofern ist nicht der gesamte statistische Zusammenhang zwischen Ursache und Wirkung auf die Störvariable zurückzuführen. In dieser Situation ist der durch die Störvariable erklärte Teil der Varianz der Wirkung geringer als in Situation 1, so dass Varianz übrig bleibt, die durch x erklärt wird.
Abbildung 4: Korrelationen (Standardisierte Regressionskoeffizienten) in Situation 3
Fazit
Eine Regression, die im Regressionsansatz gleichzeitig Ursache und Störvariable enthält, berechnet mit dem (standardisierten) Regressionskoeffizienten der Ursache den statistischen Zusammenhang zwischen Ursache und Wirkung, der um den Einfluss dieser Störvariable bereinigt ist. Dieser Koeffizient ist neben der Korrelation zwischen Ursache und Wirkung bestimmt durch die Korrelation zwischen Ursache und Störvariable sowie durch die Korrelation der Störvariable mit der Wirkung, falls Ursache und Störvariable korrelieren. Bei mehreren Störvariablen kann analog vorgegangen werden, indem diese gemeinsam mit der Ursache in den Regressionsansatz aufgenommen werden.
Beitrag aus planung&analyse 13/2 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Bortz, J.; Schuster, C.: Partielle Korrelation und multiple lineare Regression. In: Statistik für Human- und Sozialwissenschaftler, 7. Auflage, Berlin, Heidelberg, 2010, S. 339-361.
Firebaugh, G.: The Fifth Rule: Compare Like With Like. In: Seven Rules for Social Research, Princeton, Oxford, 2008, S. 120-164.
<
Share
